LeetCode 23 - Merge k Sorted Lists

發表於 分類於 Disqus：

題目

題目連結：https://leetcode.com/problems/merge-k-sorted-lists/

合併 k 個已排序好的鏈結串列成一個排序好的鏈結串列。

範例說明

1
2
3
4
5
6
7
Input:
[
  1->4->5,
  1->3->4,
  2->6
]
Output: 1->1->2->3->4->4->5->6

想法

以下簡稱 Linked list 為串列。

方法一：時間複雜度 O(KN)、空間複雜度 O(KN)

合併兩個長度分別為 N, M，排序好的串列，我們可以用雙指針遍歷兩個串列，每次都將比較小的值加入一個新的序列中，時間複雜度為 O(N + M)，空間複雜度為 O(N + M)。見下圖：

假設所有串列之總長為 N。

如果每次逐次將第一、二個串列合併，再將合併結果與第三個串列合併、再將合併結果與第四個串列合併，最終我們合併了 k - 1 次，每次合併的時間複雜度不超過 O(N)。

所以總時間複雜度為 O(KN)，空間複雜度為 O(KN)。

方法二：時間複雜度 O(NlogK)、空間複雜度 O(1)

先考慮合併序列的方法，若改為先將串列兩兩配對合併，下一輪再將合併過後的串列兩兩配對合併…，直到剩下一個串列為止。如下圖：

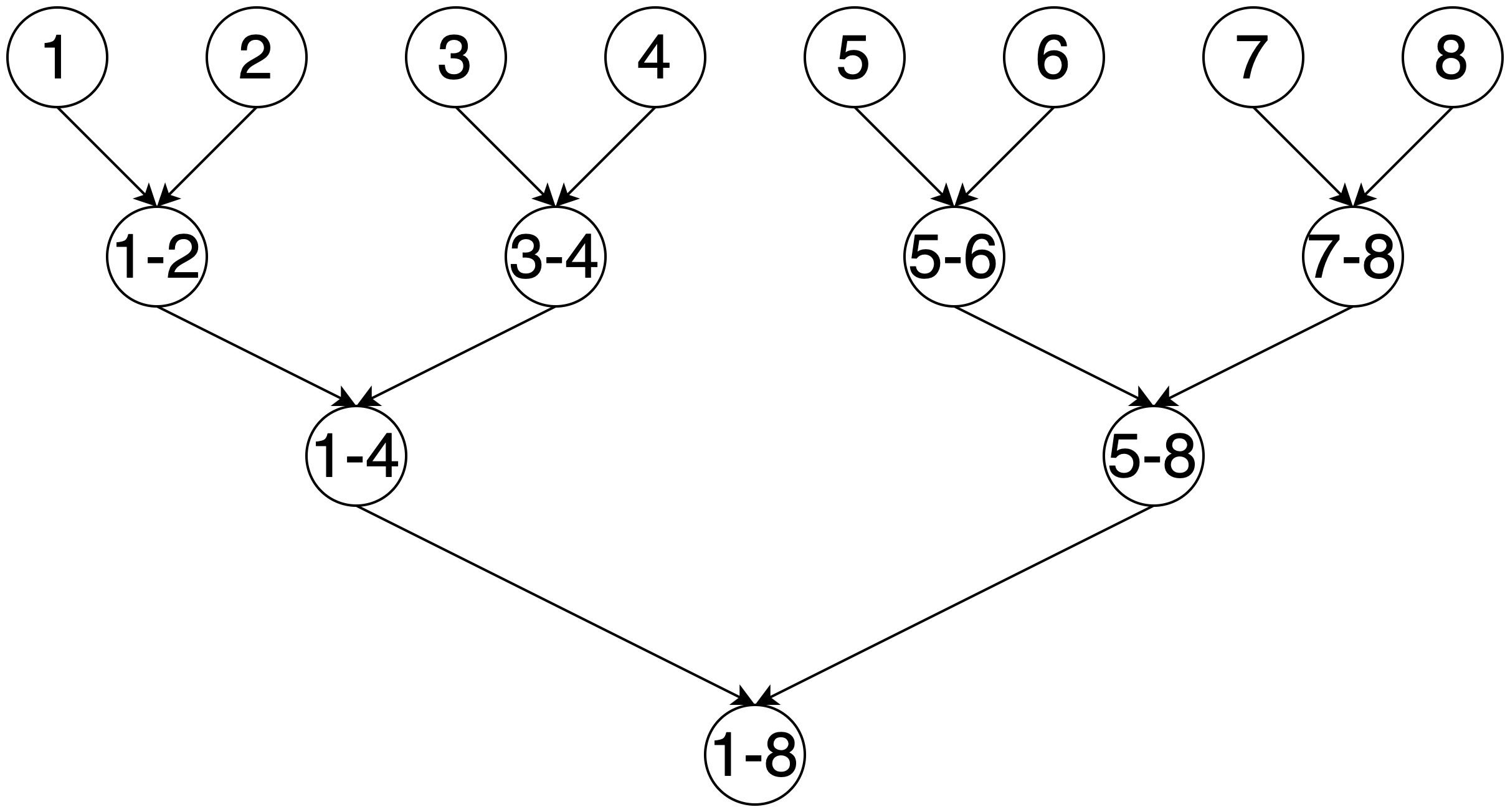
每一輪合併，串列的數量減半，總共合併了 logK + 1 輪。再加上每一輪都會遍歷所有的串列每一個數字，總長度為 N。總時間複雜度降為 O(NLogK)。

再來改善記憶體空間的使用，若合併兩序列能不花費額外的空間儲存，即可做到空間複雜度 O(1)。
解決辦法其實也很簡單，就是做 in-place（原地）合併。

合併兩串列時 lhs, rhs 時，若 lhs->val < rhs->val，則 lhs 即為合併後串列的頭，且 lhs->next 會等於合併 lhs->next, rhs 兩串列的結果。反之亦然，若 lhs->val > rhs->val，則 rhs 即為合併後串列的頭，且 rhs->next 為合併 lhs, rhs->next 兩串列的結果。

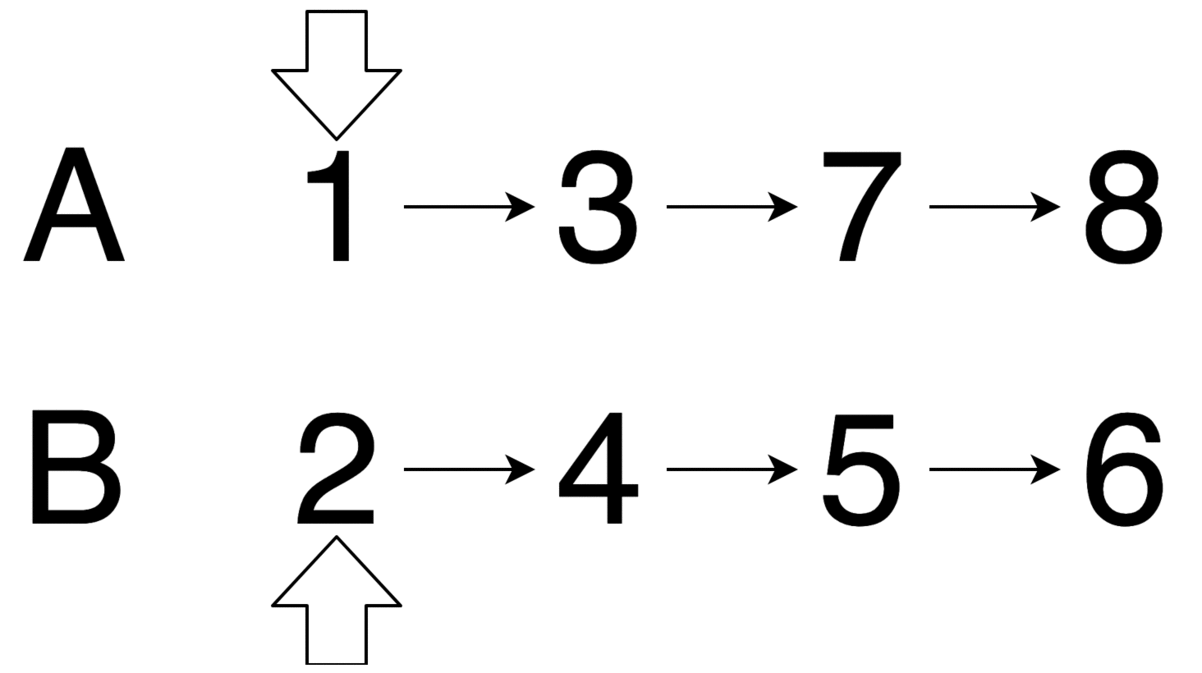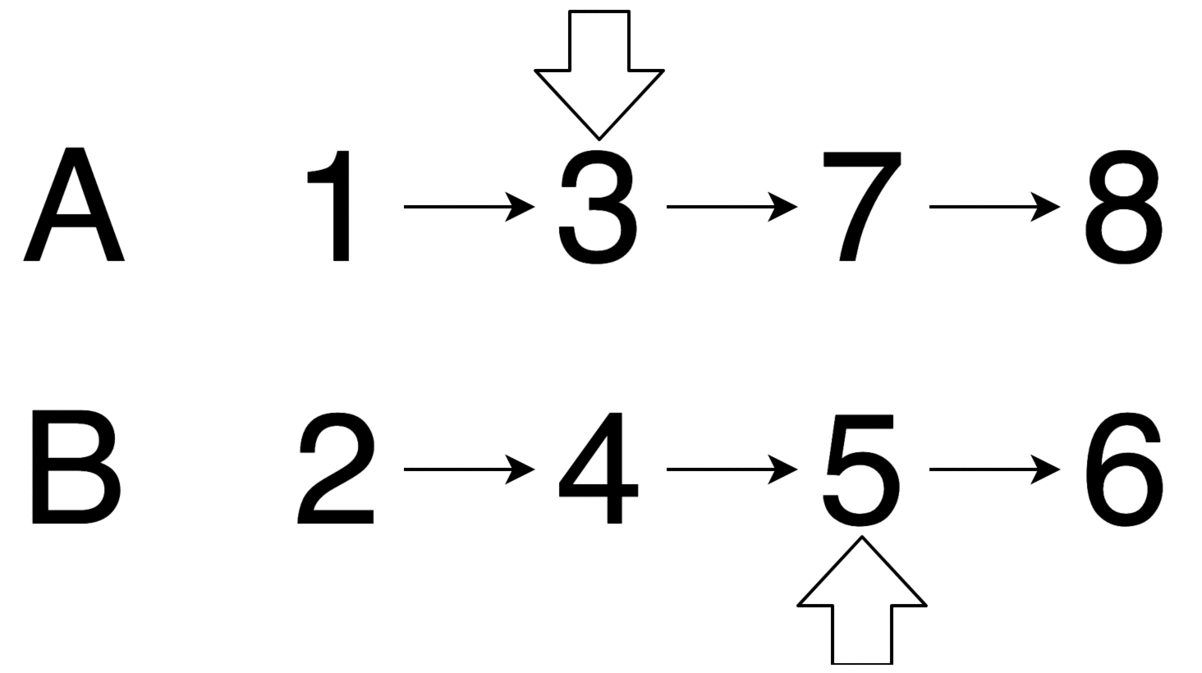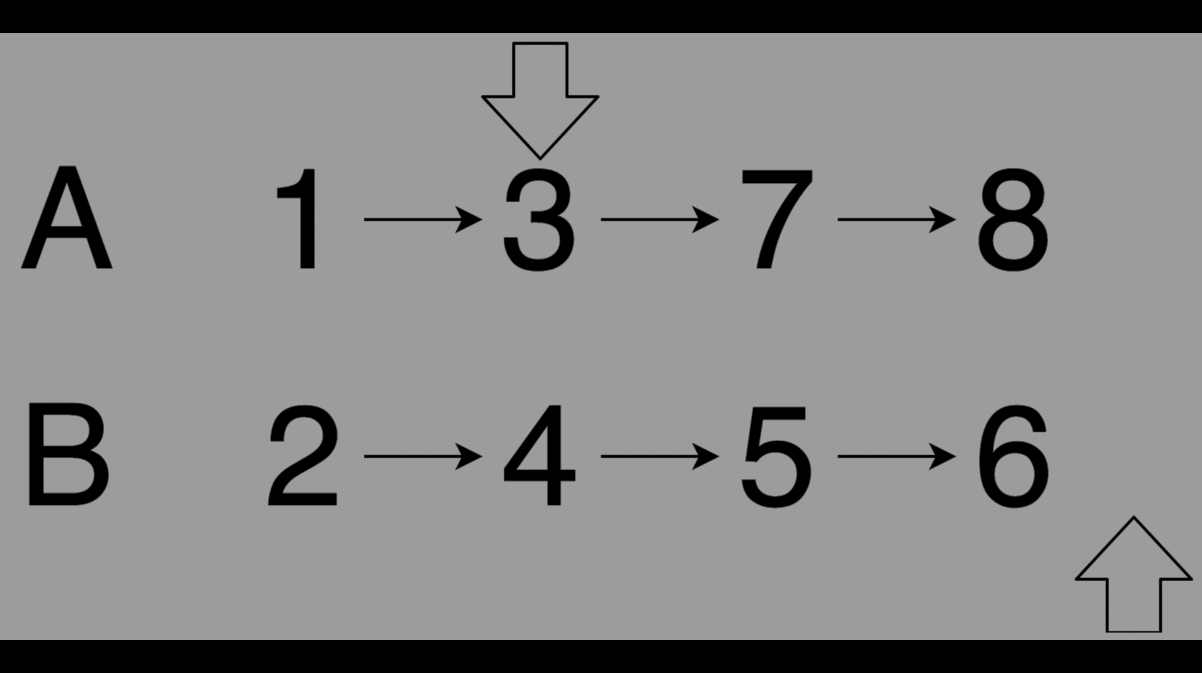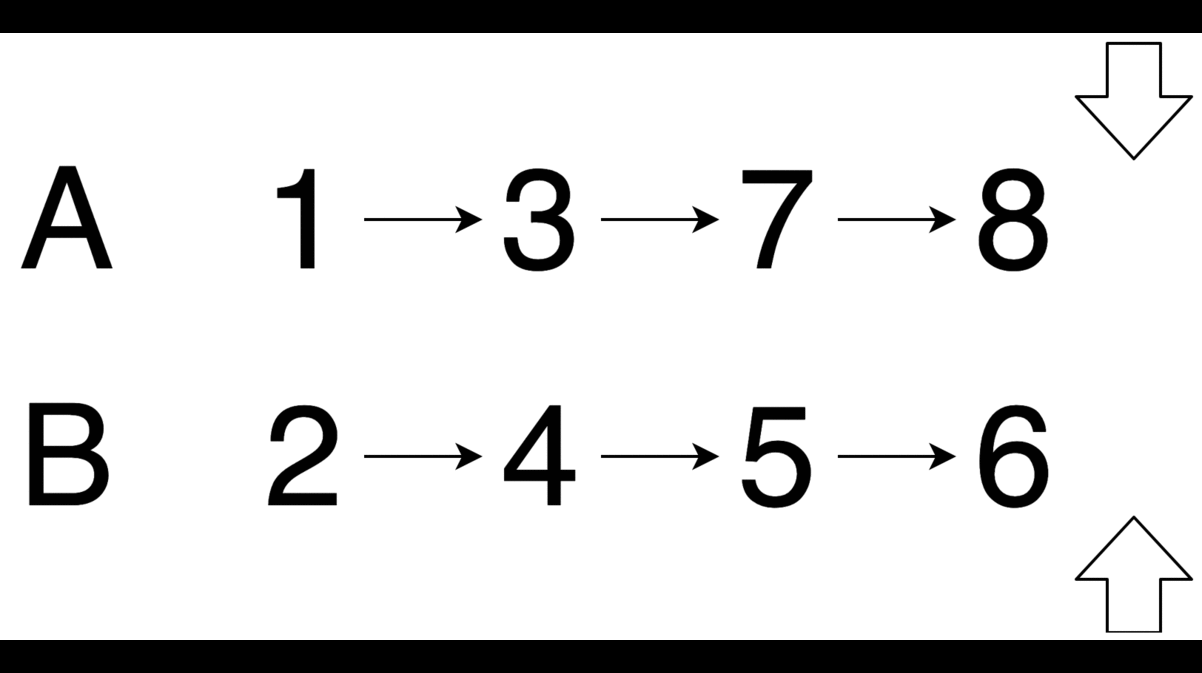
舉例來說，串列 lhs=1->3->7->8, rhs=2->4->5->6。因為 lhs->val = 1 < 2 = rhs->val，所以 lhs 為合併 lhs, rhs 後串列的頭，而 lhs->next 等於合併 lhs->next=3->7->8, rhs=2->4->5->6 兩串列的結果。

實作細節

合併 K 個串列

筆者是這樣思考的：x <- y 為將串列 y 合併進串列 x。

  • 第一輪：0 <- 1, 2 <- 3, 4 <- 5, 6 <- 7… x = 0, 2, 4, 6 ..., y = x + 1
  • 第二輪：0 <- 2, 4 <- 6, 8 <- 10, 12 <- 14… x = 0, 4, 8, 12 ..., y = x + 2
  • 第三輪：0 <- 4, 8 <- 12, 16 <- 20, 24 <- 28… x = 0, 8, 16, 24 ..., y = x + 4

總結來說，第 k 輪：

x=0, 1×(2k), 2×(2k), 3×(2k)...x=0,\ 1\times(2^k),\ 2\times(2^k),\ 3\times(2^k)...

y=x+2k−1y=x+2^{k-1}

所以：

1
2
3
4
5
6
7
8
9
10
11
// i = 2^(k-1), so i = 1, 2, 4, 8, ....
for (int i = 1; i < listsLength; i <<= 1) {
  /**
   * j = 0, 1 * (2^k), 2 * (2^k), 3 * (2^k), so
   * x = j, y = i + j
   * so we merge lists[i + j] into lists[j]
   */
  for (int j = 0; j + i < listsLength; j += i * 2) {
    lists[j] = inplaceMerge(lists[j], lists[j + i]);
  }
}

合併兩個串列

寫成遞迴的形式，見下方程式碼 inplaceMerge。

程式碼

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
/**
 * Author: justin0u0<[email protected]>
 * Problem: https://leetcode.com/problems/merge-k-sorted-lists/
 * Runtime: 28ms
 */

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
private:
  ListNode* inplaceMerge(ListNode* lhs, ListNode* rhs) {
    if (!lhs) return rhs;
    if (!rhs) return lhs;

    if (lhs->val < rhs->val) {
      // 如果 lhs->val < rhs->val, lhs->next 為合併 lhs->next, rhs 之結果
      lhs->next = inplaceMerge(lhs->next, rhs);
      // 如果 lhs->val < rhs->val，lhs 為合併兩串列之頭
      return lhs;
    } else {
      rhs->next = inplaceMerge(lhs, rhs->next);
      return rhs;
    }
  }
public:
  ListNode* mergeKLists(vector<ListNode*>& lists) {
    if (lists.empty()) return nullptr;
    int listsLength = (int)lists.size();
    // i = 2^(k-1), so i = 1, 2, 4, 8, ....
    for (int i = 1; i < listsLength; i <<= 1) {
      /**
      * j = 0, 1 * (2^k), 2 * (2^k), 3 * (2^k), so
      * x = j, y = i + j
      * so we merge lists[i + j] into lists[j]
      */
      for (int j = 0; j + i < listsLength; j += i * 2) {
        lists[j] = inplaceMerge(lists[j], lists[j + i]);
      }
    }
    return lists[0];
  }
};