LeetCode 141 - Linked List Cycle

發表於 2021-03-02 分類於 LeetCode Disqus：

題目

題目連結：https://leetcode.com/problems/linked-list-cycle/

給一個 Linked list，判斷有沒有環。

範例說明

Example 1:

1
2
3

Input: head = [3,2,0,-4], pos = 1
Output: true
Explanation: There is a cycle in the linked list, where the tail connects to the 1st node (0-indexed).

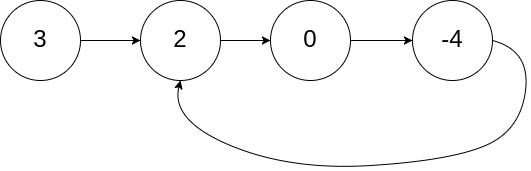
Example 2:

1
2
3

Input: head = [1,2], pos = 0
Output: true
Explanation: There is a cycle in the linked list, where the tail connects to the 0th node.

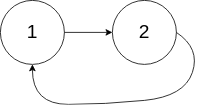
Example 3:

1
2
3

Input: head = [1], pos = -1
Output: false
Explanation: There is no cycle in the linked list.

想法

一般的作法：Time `O(N)`, Space `O(N)`

有無環的區別就是遍歷 Linked list 時是否會經過重複的位置。

最簡單的想法是使用一個指標 cur 從頭遍歷整個 Linked list，並且將 cur 的記憶體位置都記錄下來（先假設記錄在一個變數 box 內），每次都檢查 box 內有與 cur 相同的記憶體位置。

這個 box 如果是一個陣列，判斷 box 內有與 cur 相同的記憶體位置就需要遍歷整個 box 陣列，會讓整體時間複雜度變為 O(N^2)。

這個 box 可以是一個 Hash table，那麼判斷 box 內有與 cur 相同的記憶體位置 只需要 O(1)，整體時間複雜度等於遍歷一遍 Linked list 的時間 O(N)。

C++ box 可以使用 std::unordered_set<ListNode*>，但是要實作 ListNode* 的 compare 函數才能使用。

最佳的作法：Time `O(N)`, Space `O(1)`

首先，若 Linked list 有環，則一個指標不管走多少步都會被卡在環上一直繞圈。

利用這個性質，使用兩個指標，皆從頭開始遍歷。一個一次走一步，稱之為 slow；另一個一次走兩步，稱之為 fast。可以知道若存在環，不管走多少步，slow 以及 fast 都會一直在環上繞圈，並且因為 fast 每次比 slow 多走一步，所以最後 slow 以及 fast 一定會相會。

時間複雜度的部分，可以知道 slow 以及 fast 在 N 步之內一定會走到環上，並且 fast 每次與 slow 縮減一步的距離，而環的長度小於 N，因此 slow 與 fast 都到達環上後，一定會在 N 步內相會。總時間複雜度為 O(2N) = O(N)。

而沒有環時，fast 會直接走到底，也就是 null。

實作細節

注意迴圈的條件，因為 fast 會一次走兩步，所以有兩個判斷條件： fast != nullptr && fast->next != nullptr。

至於 slow 因為走的比 fast 還要慢，因此不需要判斷。

程式碼

/**
 * Author: justin0u0<[email protected]>
 * Problem: https://leetcode.com/problems/linked-list-cycle/
 * Runtime: 8ms
 */

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */

class Solution {
public:
  bool hasCycle(ListNode *head) {
    if (head == nullptr)
      return false;

    ListNode* slow = head;
    ListNode* fast = head;
    while (fast != nullptr && fast->next != nullptr) {
      slow = slow->next;
      fast = fast->next->next;
      if (slow == fast) {
        return true;
      }
    }
    return false;
  }
};

題目