LeetCode 84 - Largest Rectangle in Histogram

發表於 2020-07-20 分類於 LeetCode Disqus：

題目

題目連結：https://leetcode.com/problems/largest-rectangle-in-histogram/

給定 N 個長條圖的條的高度，每個條的寬度為 1，求最大的長方形面積。

範例說明

Example:

Input: [2,1,5,6,2,3]
Output: 10

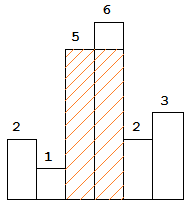
想法

時間複雜度 O(N)

首先，最大的矩形之高度一定是以某一個條的高度為高，向左右延伸直到不能再延伸為止。

要證明這個特性並不難，若當前的矩形不以任何一個條的高度為高，則矩形可以增高、變得更大。若當前矩形還可以向左右延伸，則矩形可以增加寬度，也會變得更大。所以最大的矩形之高度一定是以某一個條的高度為高，並向左右延伸直到不能再延伸為止。

接著就是要算出以位置 i 的高度 heights[i] 為高，最多可以延伸左右至哪裡。

可以發現，位置 i 向左最多可以延伸直到第一個高度比 heights[i] 小的位置。也就是如果由左到右維護一個遞增的序列，就可以知道向左延伸的極限位置。

舉範例 [2, 1, 5, 6, 2, 3] 來說，一開始遞增序列為空：

[2]：2 加入序列，序列保持遞增。數字 2 可以延伸至最左
[1]：1 加入序列，為了讓序列保持遞增，必須將 2 移除。數字 1 可以延伸至最左
[1, 5]：5 加入序列，序列保持遞增。數字 5 可以延伸至數字 1 之右側
[1, 5, 6]：6 加入序列，序列保持遞增。數字 6 可以延伸至數字 5 之右側
[1, 2]：2 加入序列，為了讓序列保持遞增，將 6, 5 依序移除。數字 2 可以延伸至數字 1 之右側
[1, 2, 3]：3 加入序列，序列保持遞增。數字 3 可以延伸至數字 2 之右側

因為上述的序列操作中，數字只會從序列的最右邊加入，且要維護遞增序列即是比較序列的右側與當前值，若當前值較小則不斷移除序列右側元素。這種先進後出（FILO）的性質可以利用一個堆疊（Stack）來維護。

反之，要計算位置 i 向右最多可以延伸至多少，則由右至左維護一個遞增的序列。

可以發現，由左至右，一個元素最多會被加入、移除 stack 一次。由右至左也是。所以總時間複雜度為 O(N)。

優化到 One Pass O(N) 的想法

2021/03/15 更新

原想法為先由左到右求出當前高度 heights[i] 能夠向左延伸到哪裡，再由右到左求出 heights[i] 向右能延伸到哪裡。

但其實 heights[i] 能向右延伸到哪裡不需要由右到左來求出，可以發現由左到右維護一個遞增的序列時，若當前的數字為 y 且數字 x 要從序列中被移除時，則 x 最多就能向右延伸到 y。

詳細做法見最後的程式碼。

實作細節

筆者原用 std::stack 來實作，不過速度較慢，所以改為使用一陣列配合一指標來模擬 stack 的運作。因此以下以講解陣列模擬 stack 的版本為主，但 std::stack 之版本也會在下面附上。

stk 為維護遞增序列用之堆疊，idx 為當前 stack 的頂端元素的索引值。其中 idx = 0 代表 stack 為空，而 stack 內的元素從索引值 1 開始放置。注意筆者是將序列的索引加入 stk 之中，而非高度。

利用 left 陣列保存位置 i 最多可以延伸多少長度。

由左至右，當 stack 不為空且其頂端元素大於等於當前的高度，則為了要保持嚴格遞增，將 stack 之頂端元素移除，並再次檢查。也就是：

1	while (idx && heights[stk[idx]] >= heights[i]) --idx;

接著，若 stack 為空，則當前元素可以向左延伸至最左，其長度為 i + 1；若 stack 不為空，則當前元素可以向左延伸至 stack 內的頂端元素位置的右側，其長度為 i - stk[idx]。也就是：

1 2	if (!idx) left[i] = i + 1; else left[i] = i - stk[idx];

最後，將當前的索引加入序列之中，也就是：

1	stk[++idx] = i;

計算向右延伸之長度時，則由右到左維護遞增序列。但是筆者沒有紀錄 right[i] 而是一計算出向右延伸之長度 right 後，直接計算當前面積 (right + left[i] - 1) * heights[i]。注意因為向左、向右延伸之長度都會覆蓋到自己本身，所以要減一。

程式碼

陣列模擬 Stack

/**
 * Author: justin0u0<[email protected]>
 * Problem: https://leetcode.com/problems/largest-rectangle-in-histogram/
 * Rumtime: 20ms
 */

class Solution {
public:
  int largestRectangleArea(vector<int>& heights) {
    int n = (int)heights.size();
    // left[i] 代表位置 i 可以向左延伸的長度
    vector<int> left(n);
    // 陣列模擬 stack，idx 為陣列頂端元素，idx = 0 代表 stack 為空。因 stack 從 1 開始編號，其長度需多 1
    vector<int> stk(n + 1);
    int idx = 0;

    // 由左至右 
    for (int i = 0; i < n; i++) {
      // 維護遞增序列
      while (idx && heights[stk[idx]] >= heights[i]) --idx;
      // 計算向左延伸之長
      if (!idx) left[i] = i + 1;
      else left[i] = i - stk[idx];
      // 將當前索引加入 stack 之中
      stk[++idx] = i;
    }
    // 清空 stack 給下一個步驟使用
    idx = 0;

    // 紀錄最大面積用
    int largestArea = 0;
    // 由右至左
    for (int i = n - 1; i >= 0; i--) {
      // 維護遞增序列
      while (idx && heights[stk[idx]] >= heights[i]) --idx;
      
      // right 即 right[i]，代表位置 i 可以向右延伸的長度，但不開陣列紀錄
      int right;
      // 計算向右延伸之長
      if (!idx) right = n - i;
      else right = stk[idx] - i;
      // 將當前索引加入 stack 之中
      stk[++idx] = i;

      // 計算面積、更新最大面積
      largestArea = max(largestArea, (right + left[i] - 1) * heights[i]);
    }
    return largestArea;
  }
};

std::stack

/**
 * Author: justin0u0<[email protected]>
 * Problem: https://leetcode.com/problems/largest-rectangle-in-histogram/
 * Rumtime: 36ms
 */

class Solution {
public:
  int largestRectangleArea(vector<int>& heights) {
    int n = (int)heights.size();
    vector<int> left(n);
    stack<int> stk;

    for (int i = 0; i < n; i++) {
      while (!stk.empty() && heights[stk.top()] >= heights[i]) stk.pop();
      if (stk.empty()) left[i] = i + 1;
      else left[i] = i - stk.top();
      stk.push(i);
    }
    while (!stk.empty()) stk.pop();

    int largestArea = 0;
    for (int i = n - 1; i >= 0; i--) {
      while (!stk.empty() && heights[stk.top()] >= heights[i]) stk.pop();
      int right;
      if (stk.empty()) right = n - i;
      else right = stk.top() - i;
      stk.push(i);

      largestArea = max(largestArea, (right + left[i] - 1) * heights[i]);
    }
    return largestArea;
  }
};

One Pass O(N) with std::stack

2021/03/15 更新

/**
 * Author: justin0u0<[email protected]>
 * Problem: https://leetcode.com/problems/largest-rectangle-in-histogram/
 */

class Solution {
public:
  int largestRectangleArea(vector<int>& heights) {
    heights.emplace_back(0); // 為了要計算到所有的 heights，因此在最後加入一個高度為 0 的使 stack 內一定會被 pop 到空
    int n = (int)heights.size();
    stack<int> stk;

    int maxArea = 0;
    for (int i = 0; i < n; i++) {
      while (!stk.empty() && heights[i] < heights[stk.top()]) {
        // 編號 idx 的數字要被 pop
        int idx = stk.top(); 
        stk.pop();
        // 以當前的高度最多可以：向左延伸到遞增序列的上一個數字，向右延伸到當前的數字
        int width = (stk.empty()) ? i : (i - stk.top() - 1);
        maxArea = max(maxArea, heights[idx] * width);
      }
      stk.push(i);
    }
    return maxArea;
  }
};