題目
題目連結:https://leetcode.com/problems/freedom-trail/
給定一個環狀的字串 ring,再給一個字串 key,要求利用 ring 在最少步數內拼出字串 key。
一開始指標在字串 ring 的第一個字元上,將指標順時鐘或是逆時鐘動一格算是一步。當指標所指的字元等於你要拼的 key 中的字元,你還必須花一步來按下確認按鈕。
範例說明
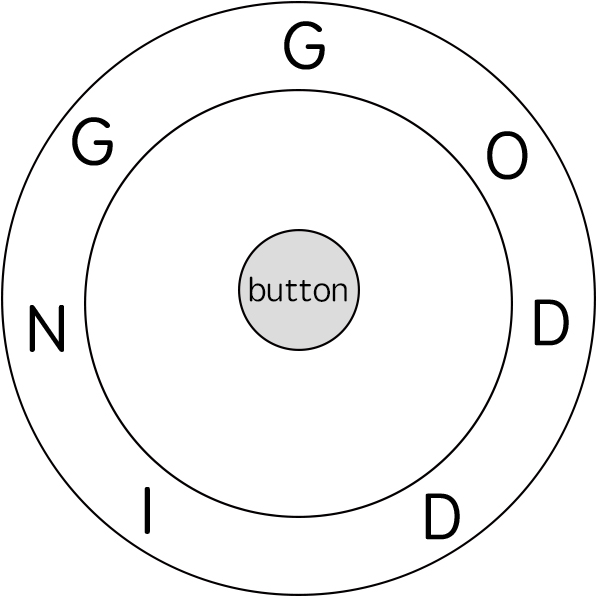
![]()
輸入:
ring = "godding"
key = "gd"
輸出: 4
說明: 一開始指標在 ring 的第一個字元 g,所以我們只要花一步按下確認鈕就好。再來我們花費兩步逆時針旋轉 ring 兩次,讓指標到達 d。再花一步按下確認鈕,總共花費 4 步。
想法
ring 中的字元是會重複的,因此我們無法確定離當前指標比較近的目標字元會使我們的答案最佳化。
因此我們換個想法,如果在搜尋第 i 個字元 key[i] 時,旋轉到位置 j 的最佳答案,紀錄為 dp(i, j)。
定義 N = ring 的長度, M = key 的長度。
定義將 ring 從位置 k 轉到位置 j 的最小花費為 dist(k, j)。那麼我們可以輕易發現:
dp(i,j)=min(dp(i−1,k)+dist(k,j)+1),∀i∈[1,M] ,∀j∈[0,N)
也就是 dp(i, j) 等於從第 i - 1 步的任意位置轉到位置 j 的花費加上原來記錄的最小花費dp(i - 1, k),再加上一步按確認鍵。
初始化時只要將 dp(0, 0) 設成 0,其餘位置設成無限大,dp(i, j) 只在 ring[j] = key[i] 時計算。便能求出答案為:
min(dp(M,j)),∀ j∈[0,N)
總時間複雜度為 O(N^2 * M)。
程式碼
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
|
class Solution {
private:
const int INF = 0x3f3f3f3f;
public:
int findRotateSteps(string ring, string key) {
const int rl = (int)ring.length();
const int kl = (int)key.length();
vector<vector<int>> dp(kl + 1, vector<int>(rl, INF));
dp[0][0] = 0;
for (int i = 1; i <= kl; i++) {
for (int j = 0; j < rl; j++) {
if (key[i - 1] == ring[j]) {
for (int k = 0; k < rl; k++) {
int dist = abs(k - j);
dp[i][j] = min(dp[i][j], dp[i - 1][k] + min(dist, rl - dist) + 1);
}
}
}
}
int steps = INF;
for (int i = 0; i < rl; i++) {
steps = min(steps, dp[kl][i]);
}
return steps;
}
};
|